Shared Memory

鲁老师大约 6 分钟GPU

我们知道，CPU和GPU组成异构计算架构，如果想从内存上优化程序，我们必须尽量减少主机与GPU设备间的数据拷贝，并将更多计算从主机端转移到GPU设备端，我们要尽量在设备端初始化数据，并计算中间数据，并尽量不做无意义的数据回写。

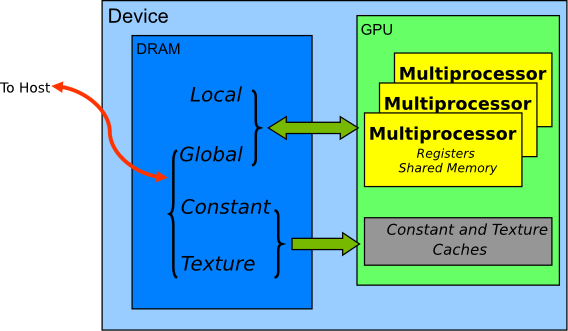
GPU的内存结构如图所示：GPU的计算核心都在Streaming Multiprocessor（SM）上，SM里有计算核心可直接访问的寄存器（Register）和共享内存（Shared Memory）；多个SM可以读取显卡上的显存，包括全局内存（Global Memory）。每个SM上的Shared Memory相当于该SM上的一个缓存，一般都很小，Telsa V100的Shared Memory也只有96KB。注意，Shared Memory和Global Memory的字面上都有共享的意思，但是不要将两者的概念混淆，Shared Memory离计算核心更近，延迟很低；Global Memory是整个显卡上的全局内存，延迟高。

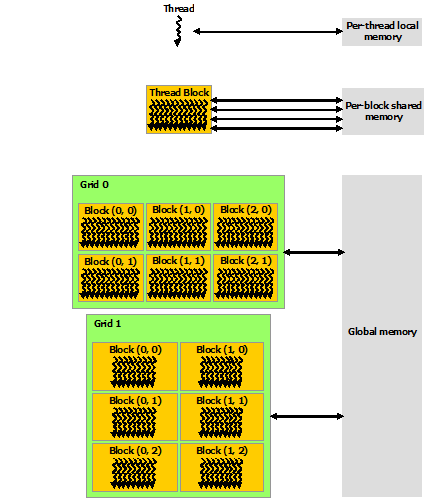
从软件角度来看，CUDA的线程可以访问不同级别的存储，每个Thread有独立的私有内存；每个Block中多个Thread都可以在该Block的Shared Memory中读写数据；整个Grid中所有Thread都可以读写Global Memory。Shared Memory的读写访问速度会远高于Global Memory。内存优化一般主要利用Shared Memory技术。下文将以矩阵乘法为例，展示如何使用Shared Memory来优化程序。

普通矩阵乘法

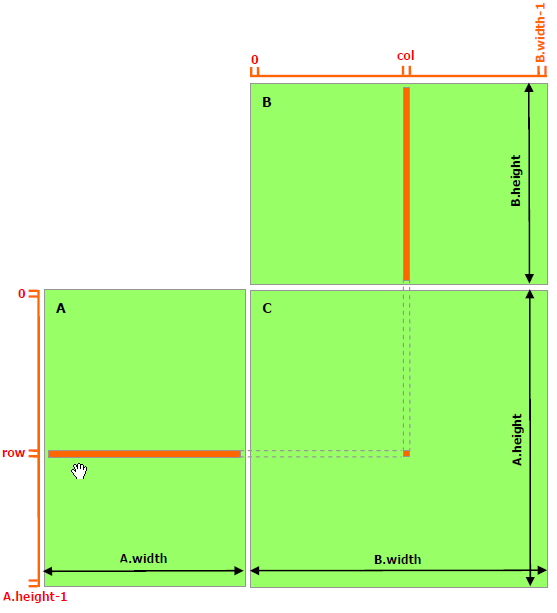
一个C = AB的矩阵乘法运算，需要我们把A的某一行与B的某一列的所有元素一一相乘，求和后，将结果存储到结果矩阵C的(row, col)上。在这种实现中，每个线程都要读取A的一整行和B的一整列，共计算M行*P列。以计算第row行为例，计算C[row, 0]、C[row, 1]...C[row, p-1]这些点时都需要从显存的Global Memory中把整个第row行读取一遍。可以算到，A矩阵中的每个点需要被读 B.width 次，B矩阵中的每个点需要被读 A.height 次。这样比较浪费时间。因此，可以将多次访问的数据放到Shared Memory中，减少重复读取的次数，并充分利用Shared Memory的延迟低的优势。

from numba import cuda
import numpy as np
import math
from time import time

@cuda.jit
def matmul(A, B, C):
    """  矩阵乘法 C = A * B
    """
    # Numba库提供了更简易的计算方法
    # x, y = cuda.grid(2)
    # 具体计算公式如下
    row = cuda.threadIdx.x + cuda.blockDim.x * cuda.blockIdx.x
    col = cuda.threadIdx.y + cuda.blockDim.y * cuda.blockIdx.y
    
    
    if row < C.shape[0] and col < C.shape[1]:
        tmp = 0.
        for k in range(A.shape[1]):
            tmp += A[row, k] * B[k, col]
        C[row, col] = tmp
        
def main():
    # 初始化矩阵
    M = 6000
    N = 4800
    P = 4000
    A = np.random.random((M, N)) # 随机生成的 [M x N] 矩阵
    B = np.random.random((N, P)) # 随机生成的 [N x P] 矩阵
    
    start = time()
    A = cuda.to_device(A)
    B = cuda.to_device(B)
    C_gpu = cuda.device_array((M, P))

    # 执行配置
    threads_per_block = (16, 16)
    blocks_per_grid_x = int(math.ceil(A.shape[0] / threads_per_block[0]))
    blocks_per_grid_y = int(math.ceil(B.shape[1] / threads_per_block[1]))
    blocksPerGrid = (blocks_per_grid_x, blocks_per_grid_y)
    
    # 启动核函数
    matmul[blocksPerGrid, threads_per_block](A, B, C_gpu)

    # 数据拷贝
    C = C_gpu.copy_to_host()
    cuda.synchronize()

    print("gpu matmul time :" + str(time() - start))

    start = time()
    C_cpu = np.empty((M, P), np.float)
    np.matmul(A, B, C_cpu)
    print("cpu matmul time :" + str(time() - start))

    # 验证正确性
    if np.allclose(C_cpu, C):
        print("gpu result correct")

if __name__ == "__main__":
    main()

基于Shared Memory的矩阵乘法

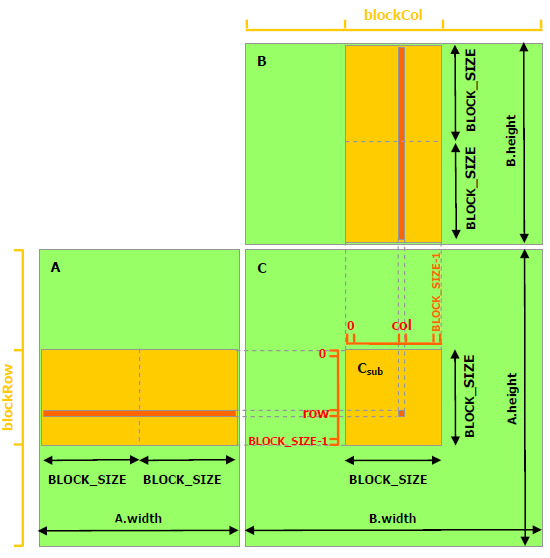
接下来的程序利用了Shared Memory来做矩阵乘法。这个实现中，跟未做优化的版本相同的是，每个Thread计算结果矩阵中的一个元素，不同的是，每个CUDA Block会以一个 BLOCK_SIZE * BLOCK_SIZE 子矩阵为基本的计算单元。具体而言，需要声明Shared Memory区域，数据第一次会从Global Memory拷贝到Shared Memory上，接下来可多次重复利用Shared Memory上的数据。

from numba import cuda, float32
import numpy as np
import math
from time import time

# thread per block
# 每个block有 BLOCK_SIZE x BLOCK_SIZE 个元素
BLOCK_SIZE = 16

@cuda.jit
def matmul(A, B, C):
    """  矩阵乘法 C = A * B
    """
    row = cuda.threadIdx.x + cuda.blockDim.x * cuda.blockIdx.x
    col = cuda.threadIdx.y + cuda.blockDim.y * cuda.blockIdx.y
    
    if row < C.shape[0] and col < C.shape[1]:
        tmp = 0.
        for k in range(A.shape[1]):
            tmp += A[row, k] * B[k, col]
        C[row, col] = tmp

@cuda.jit
def matmul_shared_memory(A, B, C):
    """
    使用Shared Memory的矩阵乘法 C = A * B
    """
    # 在Shared Memory中定义向量
    # 向量可被整个Block的所有Thread共享
    # 必须声明向量大小和数据类型
    sA = cuda.shared.array(shape=(BLOCK_SIZE, BLOCK_SIZE), dtype=float32)
    sB = cuda.shared.array(shape=(BLOCK_SIZE, BLOCK_SIZE), dtype=float32)
    
    tx = cuda.threadIdx.x
    ty = cuda.threadIdx.y
    row = cuda.threadIdx.x + cuda.blockDim.x * cuda.blockIdx.x
    col = cuda.threadIdx.y + cuda.blockDim.y * cuda.blockIdx.y
    
    if row >= C.shape[0] and col >= C.shape[1]:
        # 当(x, y)越界时退出
        return

    tmp = 0.
    # 以一个 BLOCK_SIZE x BLOCK_SIZE 为单位
    for m in range(math.ceil(A.shape[1] / BLOCK_SIZE)):
        sA[tx, ty] = A[row, ty + m * BLOCK_SIZE]
        sB[tx, ty] = B[tx + m * BLOCK_SIZE, col]
        # 线程同步，等待Block中所有Thread预加载结束
        # 该函数会等待所有Thread执行完之后才执行下一步
        cuda.syncthreads()
        # 此时已经将A和B的子矩阵拷贝到了sA和sB

        # 计算Shared Memory中的向量点积
        # 直接从Shard Memory中读取数据的延迟很低
        for n in range(BLOCK_SIZE):
            tmp += sA[tx, n] * sB[n, ty]

        # 线程同步，等待Block中所有Thread计算结束
        cuda.syncthreads()

    # 循环后得到每个BLOCK的点积之和
    C[row, col] = tmp

def main():
    # 初始化矩阵
    M = 6000
    N = 4800
    P = 4000
    A = np.random.random((M, N)) # 随机生成的 [M x N] 矩阵
    B = np.random.random((N, P)) # 随机生成的 [N x P] 矩阵

    A_device = cuda.to_device(A)
    B_device = cuda.to_device(B)
    C_device = cuda.device_array((M, P)) # [M x P] 矩阵

    # 执行配置
    threads_per_block = (BLOCK_SIZE, BLOCK_SIZE)
    blocks_per_grid_x = int(math.ceil(A.shape[0] / BLOCK_SIZE))
    blocks_per_grid_y = int(math.ceil(B.shape[1] / BLOCK_SIZE))
    blocks_per_grid = (blocks_per_grid_x, blocks_per_grid_y)

    start = time()
    matmul[blocks_per_grid, threads_per_block](A_device, B_device, C_device)
    cuda.synchronize()
    print("matmul time :" + str(time() - start))

    start = time()
    matmul_shared_memory[blocks_per_grid, threads_per_block](A_device, B_device, C_device)
    cuda.synchronize()
    print("matmul with shared memory time :" + str(time() - start))
    C = C_device.copy_to_host()

if __name__ == "__main__":
    main()

进行Shared Memory优化后，计算部分的耗时减少了近一半：

matmul time :1.4370720386505127
matmul with shared memory time :0.7994928359985352

在上面的实现过程中，有些地方也比较容易让人迷惑。

声明Shared Memory。这里使用了cuda.shared.array(shape,type)，shape为这块数据的向量维度大小，type为Numba数据类型，例如是int32还是float32。这个函数只能在设备端使用。定义好后，这块数据可被同一个Block的所有Thread共享。需要注意的是，这块数据虽然在核函数中定义，但它不是单个Thread的私有数据，它可被同Block中的所有Thread读写。
数据加载。每个Thread会将A中的一个元素加载到sA中，一个Block的 BLOCK_SIZE x BLOCK_SIZE 个Thread可以把sA填充满。cuda.syncthreads()会等待Block中所有Thread执行完之后才执行下一步。所以，当执行完这个函数的时候，sA和sB的数据已经拷贝好了。
数据复用。A中的某个点，只会被读取 B.width / BLOCK_SIZE 次；B中的某个点，只会被读 A.height / BLOCK_SIZE 次。for n in range(BLOCK_SIZE)这个循环做子矩阵向量乘法时，可多次复用sA和sB的数据。
子矩阵的数据汇总。我们以一个 BLOCK_SIZE x BLOCK_SIZE 的子矩阵为单位分别对A从左到右，对B从上到下平移并计算，共循环 A.width / BLOCK_SIZE 次。在某一步平移，会得到子矩阵的点积。for m in range(math.ceil(A.shape[1] / BLOCK_SIZE))这个循环起到了计算A从左到右与B从上到下点积的过程。

Shared Memory

# 普通矩阵乘法

# 基于Shared Memory的矩阵乘法

普通矩阵乘法

基于Shared Memory的矩阵乘法