线性回归的求解

前一节我们曾描述了线性回归的数学表示，最终得出结论，线性回归的机器学习过程就是一个使得损失函数最小的最优化问题求解过程。

Normal Equation

对于损失函数，可以使其导数为零，寻找损失函数的极值点。

一元线性回归

假设我们的模型只有一维数据，模型是一条直线$f(x) = ax + b$，我们共有$m$条训练数据，损失函数为误差平方和的平均数：

$$L(a, b) =\frac{1}{m} \sum_{i=1}^m[(ax^{(i)} + b) - y^{(i)}]^2 \tag{1}$$

可以对$a$和$b$分别求导，导数为0时，损失函数最小。

$$\begin{aligned} \frac{\partial}{\partial a}L(a, b) &= \frac{2}{m}\sum_{i=1}^mx^{(i)}(ax^{(i)} + b -y^{(i)}) \\ &=\frac{2a}{m}\sum_{i=1}^m{x^{(i)}}^2 + \frac{2b}{m}\sum_{i=1}^mx^{(i)}-\frac{2}{m}\sum_{i=1}^m{x^{(i)}y^{(i)}} \\ &= \frac{2}{m}(a\sum_{i=1}^m{x^{(i)}}^2 + b\sum_{i=1}^mx^{(i)} - \sum_{i=1}^m{x^{(i)}y^{(i)}}) \\ &= \frac{2}{m}(a\sum_{i}^m{x^{(i)}}^2-\sum_{i=1}^m(y^{(i)}-b)x^{(i)}) \end{aligned} \tag{2}$$

$$\begin{aligned} \frac{\partial}{\partial b}L(a, b) &= \frac{2}{m}\sum_{i=1}^max^{(i)}+b-y^{(i)} \\ &= \frac{2a}{m}\sum_{i=1}^m{x^{(i)}} + 2b - \frac{2}{m}\sum_{i=1}^m{y^{(i)}} \\ &= \frac{2}{m}(\sum_{i=1}^max^{(i)} + mb - \sum_{i=1}^my^{(i)}) \\ &= \frac{2}{m}(mb - \sum_{i=1}^m(y^{(i)} -ax^{(i)})) \end{aligned} \tag{3}$$

上面两个公式是损失函数$L$对$a$和$b$进行求偏导。当导数为0时，可以求得损失函数的最小值，即由公式2和3可以得到最优解$a^*$和$b^*$。

$$\frac{\partial}{\partial a}L(a, b) = 0 \Rightarrow \frac{2}{m}(a\sum_{i=1}^m{x^{(i)}}^2-\sum_{i=1}^m(y^{(i)}-b)x^{(i)}) = 0 \tag{4}$$

$$\frac{\partial}{\partial b}L(a, b) = 0 \Rightarrow \frac{2}{m}(mb - \sum_{i=1}^m(y^{(i)} -ax^{(i)})) = 0 \tag{5}$$

最优解为：

$$a^*=\frac{\sum_{i=1}^my^{(i)}(x^{(i)}-\bar{x})}{\sum_{i=1}^m{x^{(i)}}^2-\frac{1}{m}(\sum_{i=1}^mx^{(i)})^2} \tag{6}$$

$$b^*=\frac{1}{m}\sum_{i=1}^m(y^{(i)}-ax^{(i)})$$

其中，$\bar{x}=\frac{1}{m}\sum_{i=1}^mx^{(i)}$，即为$\boldsymbol{x}$的均值。

以上就是一元线性回归的最小二乘法求解过程。很多机器学习模型中都需要经历上述过程：确定损失函数，求使损失函数最小的参数。求解过程会用到一些简单的微积分，因此复习一下微积分中偏导数部分，有助于理解机器学习的数学原理。

多元线性回归

更为一般的情形下，特征是多维的：

$$f(\boldsymbol{x}^{(i)}) = \boldsymbol{w}^T \boldsymbol{x}^{(i)} \tag{7}$$

上面的公式中，我们其实是使用$b=w_{0}$来表示参数中的 $b$ ，将 $b$ 添加到特征向量中，将$n$维特征扩展成$n+1$维，也就是在每个 $\boldsymbol{x}^{(i)}$ 中添加一个值为1的项。各个向量和矩阵形状如公式8所示。

$$\boldsymbol{w} = \left[ \begin{array}{c} w_0\\ w_1\\ w_2\\ \vdots\\ w_n \\ \end{array} \right] \quad \boldsymbol{X} = \left[ \begin{array}{c} x^{(1)}\\ x^{(2)}\\ \vdots\\ x^{(m)} \end{array} \right] = \begin{pmatrix} 1 & x_{1}^{(1)} & x_{2}^{(1)} & \cdots & x_{n}^{(1)} \\ 1 & x_{1}^{(2)} & x_{2}^{(2)} & \cdots & x_{n}^{(2)}\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 1 & x_{1}^{(m)} & x_{2}^{(m)} & \cdots & x_{n}^{(m)} \\ \end{pmatrix} \quad \boldsymbol{y} = \left[ \begin{array}{c} y_1\\ y_2\\ \vdots\\ y_m \end{array} \right] \tag{8}$$

其中，向量 $\boldsymbol{w}$ 表示模型中各个特征的权重；矩阵 $\boldsymbol{X}$ 的每一行是一条样本，每条样本中有$n+1$个特征值，分别为该样本在不同维度上的取值；向量 $\boldsymbol{y}$ 为真实值。可以用内积的形式来表示求和项：$\sum_{j=0}^{n}w_jx_{j}^{(i)} =\boldsymbol{w}^\top \boldsymbol{x}^{(i)}$。用矩阵乘法的形式可以表示为：$\boldsymbol{y} = \boldsymbol{X}\boldsymbol{w}$。

$$y^{(i)} = \sum_{j=0}^{n}w_jx_{j}^{(i)} =\boldsymbol{w}^\top \boldsymbol{x}^{(i)} \Rightarrow \boldsymbol{y} = \boldsymbol{X}\boldsymbol{w}\tag{9}$$

一般机器学习领域更喜欢使用矩阵乘法的形式来表示一个模型，这不仅因为这样表示起来更简单，也是因为现代计算机对向量计算做了大量优化，无论是CPU还是GPU都喜欢向量计算，并行地处理数据，可以得到成百上千倍的加速比。

注

公式中不加粗的表示标量，加粗的表示向量或矩阵。

比一元线性回归更为复杂的是，多元线性回归最优解不是一条直线，是一个多维空间中的超平面，训练数据散落在超平面的两侧。

多元线性回归一般寻找最优超平面

$$L(\boldsymbol{w}) = (\boldsymbol{X}\boldsymbol{w}-\boldsymbol{y})^\top (\boldsymbol{X}\boldsymbol{w}-\boldsymbol{y}) = ||\boldsymbol{X}\boldsymbol{w}-\boldsymbol{y}||_2^2 \tag{10}$$

多元线性回归的损失函数仍然使用“预测值-真实值”的平方来计算，公式10为整个模型损失函数的向量表示。这里出现了一个竖线组成的部分，它被称作L2范数的平方。范数通常针对向量，也是一个机器学习领域经常用到的数学符号，公式11展示了一个向量 $\boldsymbol{x}$ 的L2范数的平方以及其导数。

$$\\ ||\boldsymbol{x}||_2^2 = ((\sum_{i=1}^N{x^{(i)}}^2)^{\frac{1}{2}})^2 \qquad \qquad \qquad \qquad \nabla||\boldsymbol{x}||_2^2=2\boldsymbol{x} \tag{11}\\$$

对公式10中的向量$\boldsymbol{w}$ 求导，令导数为零：

$$\frac{\partial}{\partial \boldsymbol{w}}L(\boldsymbol{w}) = 2\boldsymbol{X}^\top (\boldsymbol{X}\boldsymbol{w} - \boldsymbol{y}) = 0 \tag{12}$$

$$\boldsymbol{X}^\top\boldsymbol{X}\boldsymbol{w} = \boldsymbol{X}^\top \boldsymbol{y} \Rightarrow (\boldsymbol{X}^\top\boldsymbol{X})^{-1} \boldsymbol{X}^\top\boldsymbol{X}\boldsymbol{w}=(\boldsymbol{X}^\top\boldsymbol{X})^{-1} \boldsymbol{X}^\top \boldsymbol{y} \tag{13}$$

$$\boldsymbol{w}^* = (\boldsymbol{X}^\top\boldsymbol{X})^{-1}\boldsymbol{X}^\top \boldsymbol{y} \tag{14}$$

公式14是向量$\boldsymbol{w}$ 的解，这是一个矩阵方程。使用这种方法求最优解，其实是在解这个矩阵方程，英文中称这种方法为正规方程（Normal Equation）。

这个方法有一个问题，在线性代数课程中肯定曾提到过，$\boldsymbol{X}^\top\boldsymbol{X}$是满秩（Full-Rank）或正定（Positive Definite）时，才能解方程组。“满秩”或者“正定”到底什么意思呢？用通俗的话来讲，样本中的数据必须足够丰富，且有足够的代表性，矩阵方程才有唯一解，否则矩阵方程会有多组解。如果特征有上万维，但只有几十个样本来训练，我们很难得到一个满意的最优解。

上述方法还有一个问题：公式14中矩阵求逆的计算量比较大，复杂度在$O(n^3)$级别。当特征维度达到百万级以上或样本数量极大时，计算时间非常长，单台计算机内存甚至存储不下这些参数，求解正规方程的办法就不现实了。

前面花了点时间描述线性回归的求解过程，出现了不少公式，跟很多朋友一样，笔者以前非常讨厌看公式，看到一些公式就头大，因此觉得机器学习非常难。不过，静下心来仔细读一遍，会发现其实这些公式用到的都是微积分、线性代数中比较基础的部分，并不需要高大上的知识，理工科背景的朋友应该都能看得懂。另外，复习一下矩阵和求导等知识有助于我们理解深度学习的一些数学原理。

梯度下降法

求解损失函数最小问题，或者说求解使损失函数最小的最优化问题时，经常使用搜索的方法。具体而言，选择一个初始点作为起点，然后开始不断搜索，损失函数逐渐变小，当到达搜索迭代的结束条件时，该位置为搜索算法的最终结果。我们先随机猜测一个$\boldsymbol{w}$，然后对$\boldsymbol{w}$值不断进行调整，来让 $L(\boldsymbol{w})$ 逐渐变小，最好能找到使得 $L(\boldsymbol{w})$ 最小的 $\boldsymbol{w}$。

具体来说，我们可以考虑使用梯度下降法（Gradient Descent），这个方法就是从某一个$\boldsymbol{w}$的初始值开始，然后逐渐对权重进行更新，或者说每次用新计算的值覆盖原来的值：

$$w_j := w_j - \alpha \frac \partial {\partial{w_j}}L(\boldsymbol{w}) \tag{15}$$

这里的 $\alpha$ 也称为学习率，$\frac \partial {\partial{w_j}}L(\boldsymbol{w})$是梯度（Gradient）。微积分课中提到，在某个点，函数沿着梯度方向的变化速度最快。因为我们想最小化损失函数$L$，因此，我们每次都沿着梯度下降，不断向 $L$ 降低最快的方向移动。

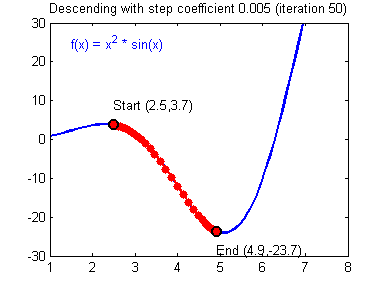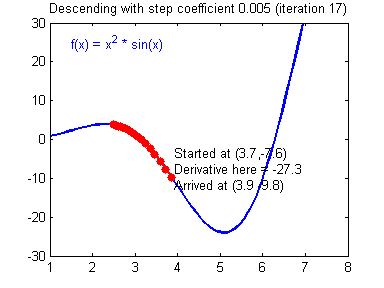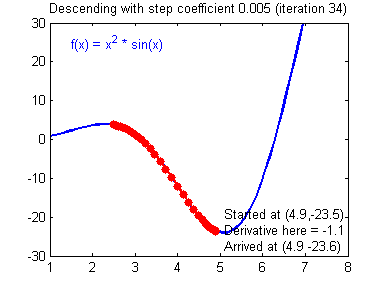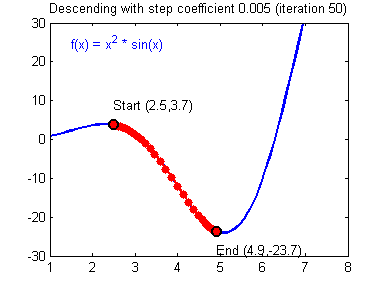
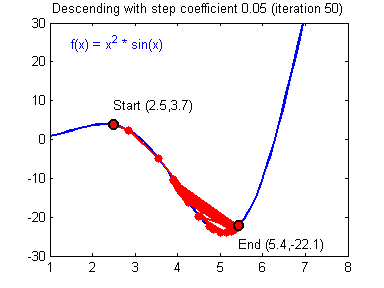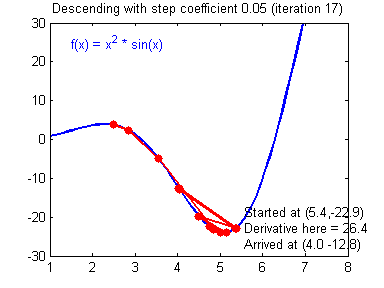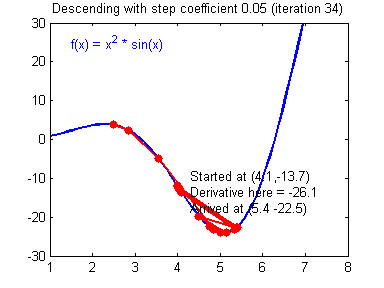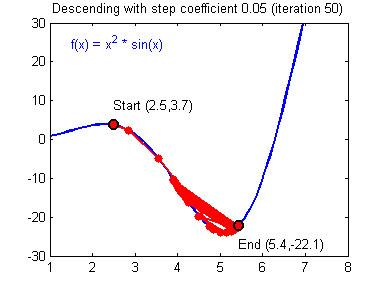
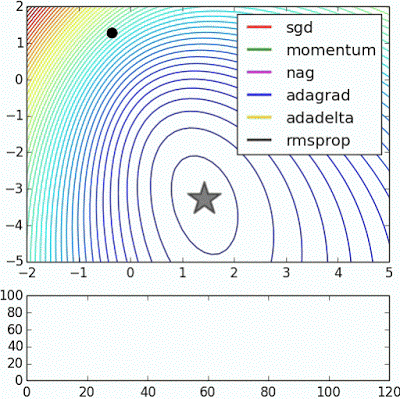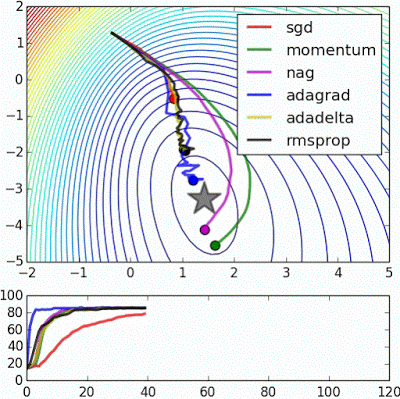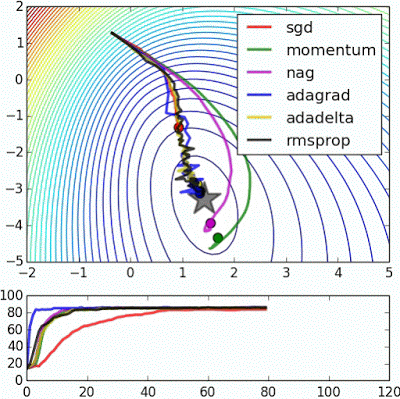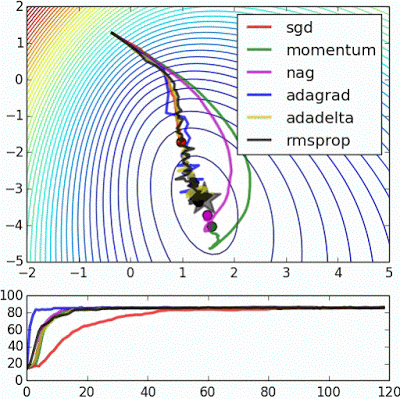
用图像直观来看，损失函数沿着梯度下降的过程如下所示。迭代过程最终收敛在了最小值附近，此时，梯度或者说导数接近0。

损失函数沿梯度下降的过程

回到学习率$\alpha$上，$\alpha$代表在某个点上，我们对梯度的置信程度。一般情况下，$0 < \alpha < 1$。$\alpha$越大，表示我们希望损失函数以更快的速度下降，$\alpha$越小，表示我们希望损失函数下降的速度变慢。如果$\alpha$设置得不合适，每次的步进太大，损失函数很可能无法快速收敛到最小值。如下所示，损失函数经过很长时间也难以收敛到最小值。在实际应用中，$\alpha$经常随着迭代次数变化而变化，比如，初始化时较大，后面渐渐变小。

收敛速度过慢的情形

我们之前提到过，$\boldsymbol{w}$是一个向量，假设它是$n$维的，在更新$\boldsymbol{w}$时，我们是要同时对 $n$ 维所有$\boldsymbol{w}$值进行更新，其中第$j$维就是使用上面的公式15。

接下来我们简单推导一下梯度公式，首先考虑只有一条训练样本 $(\boldsymbol{x}^{(i)}, y^{(i)})$ 的情况。由$L(w)=\frac{1}{2}(f(\boldsymbol{x}^{(i)})-y^{(i)})^2$，其中，$\frac{1}{2}$是常数项，不影响最优解的取值，主要是为了方便求导。可以得到：

$$\begin{aligned} \frac \partial {\partial w_j}L(\boldsymbol{w}) & = \frac \partial {\partial w_j} \frac 12(f(\boldsymbol{x}^{(i)})-y^{(i)})^2\\ & = 2 \cdot\frac 12(f(\boldsymbol{x}^{(i)})-y^{(i)})\cdot \frac \partial {\partial w_j} (f(\boldsymbol{x}^{(i)})-y^{(i)}) \\ & = (f(\boldsymbol{x}^{(i)})-y^{(i)})\cdot \frac \partial {\partial w_j}(\sum^n_{j=0} w_jx_{j}^{(i)}-y^{(i)}) \\ & = (f(\boldsymbol{x}^{(i)})-y^{(i)}) x_{j}^{(i)} \end{aligned}$$

对单个训练样本，每次对梯度的更新规则如下所示：

$$w_j := w_j - \alpha (f(\boldsymbol{x}^{(i)})-y^{(i)}) x_{j}^{(i)}$$

这个规则有几个看上去就很自然直观的特性：

• 更新的大小与$(f(\boldsymbol{x}^{(i)})-y^{(i)})$成比例。
• 当我们遇到训练样本的预测值$f(\boldsymbol{x}^{(i)})$与 $y^{(i)}$ 的真实值非常接近的情况下，就会发现基本没必要再对参数进行修改了；与此相反的情况是，如果我们的预测值 $f(\boldsymbol{x}^{(i)})$ 与 $y^{(i)}$真实值有很大的误差（比如距离特别远），那就需要对参数进行更大地调整。这也与前面所展示的梯度下降动态图中相吻合。

批量梯度下降法

当只有一个训练样本的时候，我们推导出了权重更新的规则。当一个训练集有$m$个训练样本的时候，$L(\boldsymbol{w}) = \frac{1}{2}\sum_{i=1}^m(f(\boldsymbol{x}^{(i)}) - y^{(i)})^2$。求导时，只需要对多条训练样本的数据做加和。

$$L(\boldsymbol{w}) = \frac{1}{2} \lbrace (f(\boldsymbol{x}^{(1)}) - y^{(1)})^2 + \cdots + (f(\boldsymbol{x}^{(m)}) - y^{(m)})^2 \rbrace$$

$$\begin{aligned} \frac \partial {\partial w_j}L(w) & = \frac \partial {\partial w_j} \frac 12\lbrace (f(\boldsymbol{x}^{(1)}) - y^{(1)})^2 + \cdots + (f(\boldsymbol{x}^{(m)}) - y^{(m)})^2 \rbrace\\ & = 2 \cdot\frac 12(f(\boldsymbol{x}^{(1)})-y^{(1)})\cdot \frac \partial {\partial w_j} (f(\boldsymbol{x}^{(1)})-y^{(1)}) + \cdots\\ & = (f(\boldsymbol{x}^{(1)})-y^{(1)})\cdot \frac \partial {\partial w_j}(\sum^n_{j=0} w_jx_{j}^{(1)}-y^{(1)}) + \cdots \\ & = (f(\boldsymbol{x}^{(1)})-y^{(1)}) x_{j}^{(1)} + \cdots \\ & = \sum_{i=1}^m(f(\boldsymbol{x}^{(i)}) - y^{(i)})x_{j}^{(i)} \end{aligned}$$

因此，可以得出每个$w_j$的导数：

$$w_j := w_j - \alpha \sum^m_{i=1}(f(\boldsymbol{x}^{(i)})-y^{(i)})x_{j}^{(i)}$$

具体而言，这个算法为：

$$\begin{aligned} &\quad Repeat \ k \ iterations \quad \{ \\ & \quad\quad for \ every \ \ w_j \ in \ \boldsymbol{w} \ w_j := w_j - \alpha \sum^m_{i=1}(f(\boldsymbol{x}^{(i)})-y^{(i)})x_{j}^{(i)}\quad \\ &\quad\} \end{aligned}$$

这一方法在每一次迭代时使用整个训练集中的所有样本来更新参数，也叫做批量梯度下降法（Batch Gradient Descent，BGD）。线性回归的损失函数$L$ 是一个凸二次函数（Convex Quadratic Function），凸函数的局部极小值就是全局最小值，线性回归的最优化问题只有一个全局解。也就是说，假设不把学习率 $\alpha$ 设置的过大，迭代次数足够多，梯度下降法总是收敛到全局最小值。

随机梯度下降法

批量梯度下降在更新参数时要把所有样本都要考虑进去。当数据量大、特征多时，每次迭代都使用全量数据并不现实；而且全量数据本身包含很多冗余信息，数据量越大，冗余信息越多，在求最优解时，冗余信息并没有太大帮助。一种妥协方法是，每次更新参数时，只随机抽取部分样本。一个比较极端的情况是，每次迭代时随机抽取一条样本，使用单个样本来更新本次迭代的参数，这个算法被称为随机梯度下降（Stochastic gradient descent，SGD），如下所示：

$$\begin{aligned} &\quad Repeat \ k \ iterations \quad \{ \\ & \quad\quad randomly \ choose \ i \\ & \quad\quad for \ every \ \ w_j \ in \ \boldsymbol{w} \ w_j := w_j - \alpha (f(\boldsymbol{x}^{(i)})-y^{(i)})x_{j}^{(i)}\quad \\ &\quad\} \end{aligned}$$

另外，我们也可以每次随机抽取一个小批次（Mini-batch）的训练数据，用这批数据更新本次迭代参数，这种算法被称为Mini-batch SGD。Mini-batch SGD是BGD和SGD之间的一个妥协，Mini-batch SGD降低了SGD中随机性带来的噪音，又比BGD更高效。

梯度下降法努力逼近最优解，求解速度在数据量大时有优势，但不一定能得到绝对的最优解。在很多实际应用中，虽然梯度下降求解的点在最优点附近，但其实已经能够满足需求。考虑到这些因素，梯度下降法，尤其是随机梯度下降法被大量应用在机器学习模型求解上。除了以上介绍的几种外，梯度下降法有很多变体。

不同梯度下降法的收敛速度示意图

梯度下降法的NumPy实现

前面推导了这么多，Talk is cheap，Show some code。接下来，我们使用NumPy实现一个线性回归模型，分别使用批量梯度下降和随机梯度下降。实现过程中我们会发现，有些问题是公式推导不会提及的工程问题，比如，计算过程中的数据太大，超出了float64的可表示范围。工程实现体现了理论和实践之间的差异，实际上，往往这些工程细节决定着机器学习框架的易用性。

import numpy as np

class LinearRegression:

    def __init__(self):
        # the weight vector
        self.W = None

    def train(self, X, y, method='bgd', learning_rate=1e-2, num_iters=100, verbose=False):
        """
        Train linear regression using batch gradient descent or stochastic gradient descent

        Parameters
        ----------
        X: training data, shape (num_of_samples x num_of_features), num_of_samples rows of training sample, each training sample has num_of_features-dimension features.
        y: target, shape (num_of_samples, 1). 
        method: (string) 'bgd' for Batch Gradient Descent or 'sgd' for Stochastic Gradient Descent
        learning_rate: (float) learning rate or alpha
        num_iters: (integer) number of steps to iterate for optimization
        verbose: (boolean) if True, print out the progress

        Returns
        -------
        losses_history: (list) of losses at each training iteration
        """
        num_of_samples, num_of_features = X.shape

        if self.W is None:
            # initilize weights with values
            # shape (num_of_features, 1)
            self.W = np.random.randn(num_of_features, 1) * 0.001
        losses_history = []

        for i in range(num_iters):

            if method == 'sgd':
                # randomly choose a sample
                idx = np.random.choice(num_of_samples)
                loss, grad = self.loss_and_gradient(X[idx, np.newaxis], y[idx, np.newaxis])
            else:
                loss, grad = self.loss_and_gradient(X, y)
            losses_history.append(loss)

            # Update weights using matrix computing (vectorized)
            self.W -= learning_rate * grad

            if verbose and i % (num_iters / 10) == 0:
                print('iteration %d / %d : loss %f' %(i, num_iters, loss))
        return losses_history


    def predict(self, X):
        """
        Predict value of y using trained weights

        Parameters
        ----------
        X: predict data, shape (num_of_samples x num_of_features), each row is a sample with num_of_features-dimension features.

        Returns
        -------
        pred_ys: predicted data, shape (num_of_samples, 1)
        """
        pred_ys = X.dot(self.W)
        return pred_ys


    def loss_and_gradient(self, X, y, vectorized=True):
        """
        Compute the loss and gradients

        Parameters
        ----------
        The same as self.train function

        Returns
        -------
        tuple of two items (loss, gradient)
        loss: (float)
        gradient: (array) with respect to self.W 
        """
        if vectorized:
            return linear_loss_grad_vectorized(self.W, X, y)
        else:
            return linear_loss_grad_for_loop(self.W, X, y)


def linear_loss_grad_vectorized(W, X, y):
    """
    Compute the loss and gradients with weights, vectorized version
    """
    # vectorized implementation 
    num_of_samples = X.shape[0]
    # (num_of_samples, num_of_features) * (num_of_features, 1)
    f_mat = X.dot(W)

    # (num_of_samples, 1) - (num_of_samples, 1)
    diff = f_mat - y 
    loss = 1.0 / 2 * np.sum(diff * diff)
    
    # {(num_of_samples, 1).T dot (num_of_samples, num_of_features)}.T
    gradient = ((diff.T).dot(X)).T

    return (loss, gradient)


def linear_loss_grad_for_loop(W, X, y):
    """
    Compute the loss and gradients with weights, for loop version
    """
    
    # num_of_samples rows of training data
    num_of_samples = X.shape[0]
    
    # num_of_samples columns of features
    num_of_features = X.shape[1]
    
    loss = 0
    
    # shape (num_of_features, 1) same with W
    gradient = np.zeros_like(W) 
    
    for i in range(num_of_samples):
        X_i = X[i, :] # i-th sample from training data
        f = 0
        for j in range(num_of_features):
            f += X_i[j] * W[j, 0]
        diff = f - y[i, 0]
        loss += np.power(diff, 2)
        for j in range(num_of_features):
            gradient[j, 0] += diff * X_i[j]
            
    loss = 1.0 / 2 * loss

    return (loss, gradient)

参考资料

1. Andrew Ng: CS229 Lecture Notes
2. 周志华：《机器学习》
3. https://houxianxu.github.io/2015/03/31/linear-regression-post/
4. https://www.cs.toronto.edu/~frossard/post/linear_regression/
5. https://kivy-cn.github.io/Stanford-CS-229-CN/
6. https://datawhalechina.github.io/pumpkin-book/