Learning Rate Schedule：学习率调整策略

鲁老师大约 3 分钟

学习率（Learning Rate，LR）是深度学习训练中非常重要的超参数。同样的模型和数据下，不同的LR将直接影响模型何时能够收敛到预期的准确率。

随机梯度下降SGD算法中，每次从训练数据中随机选择一批样本，样本数为Batch Size。很多实验都证明了，在LR不变的情况下，Batch Size越大，模型收敛效果越差[1]。

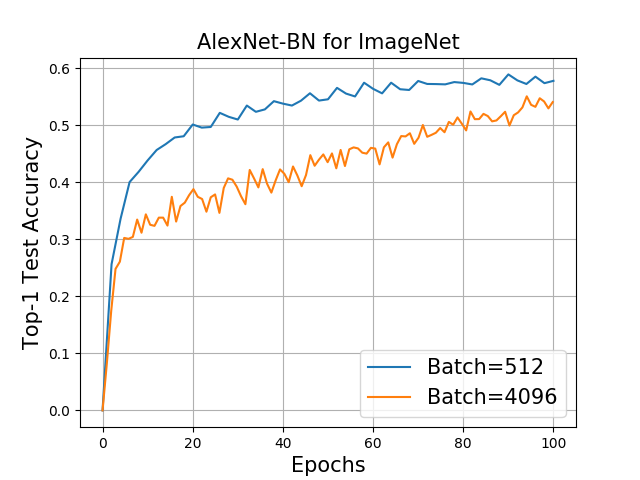
AlexNet ImageNet在不同Batch Size下的TOP1准确率

Linear Scale

随着Batch Size增大，一个Batch Size内样本的方差变小；也就是说越大的Batch Size，意味着这批样本的随机噪声越小。那么我们可以更加相信这批样本所产生的梯度，可以增大LR，在负梯度方向更快下降。有人[2]提出了根据Batch Size的大小，线性地调整LR，在ResNet50上实验有效果。例如，ResNet50论文中使用的Batch Size为256，LR为0.1，那么对于更大的Batch Size bs：

lr = 0.1 \times \frac{bs}{256}

Warmup

在训练最开始，模型中绝大多数参数都是随机初始化的，与最终模型很远。一开始就使用一个很大的LR，会增加不确定性。所以在训练最开始，先使用一个较小的LR，训练几轮Epoch后，再使用较大的LR[2]。

Decay

一直使用较大的LR也有问题，在训练中后期，过大的LR可能导致模型在最优解附近震荡，无法快速收敛。所以，在中后期，需要将LR进行一些衰减（Decay）。ResNet论文中最初使用的Step Decay：每训练30个Epoch，LR衰减为刚才的0.1倍。还有Cosine衰减[3]：最初的LR为 $lr_{init}$ ，整个训练的Step数目为 $T$ （steps_per_epoch * total_epochs），当前Step为 $t$ ，当前的 $lr_{t}$ 由下面公式计算得到。

lr_{t} = \frac{1}{2}(1+ \cos{(\frac{t\pi}{T}}))\times lr_{init}

Step Decay和Cosine Decay的LR随着训练Epoch变化如下：

Step Decay与Cosine Decay，初始LR为0.1

Linear + Warmup + Decay

将以上三种LR策略组合起来，可以形成一个完整的LR策略：根据Batch Size大小，线性地缩放LR基准值，前几个Epoch使用较小的LR先进行Warmup，之后从LR基准值开始，逐渐对LR进行衰减。比如，ResNet50 ImageNet下Batch Size为1024，LR基准值为0.4 = 0.1 * (1024 / 256)，整个训练过程中的LR策略如下图所示：

Batch Size为1024，LR基准值为0.4，Warmup + Decay

TOP1准确率如下图：

ResNet50 ImageNet TOP1准确率

训练过程中间部分Cosine策略的LR接近线性下降，而Step策略0.1倍地下降；从TOP1准确率来看，Step策略提升更快，直到最后Cosine策略与Step策略的LR近乎相同，TOP1准确率也接近相同。

B. Ginsburg, I. Gitman, and Y. You. Large batch training of convolutional networks with layer-wise adaptive rate scaling. 2018
P. Goyal, P. Dollar, R. B. Girshick, P. Noordhuis, L. Wesolowski, A. Kyrola, A. Tulloch, Y. Jia, and K. He. Accurate, large minibatch SGD: training imagenet in 1 hour. 2017
I. Loshchilov and F. Hutter. SGDR: stochastic gradient de-scent with restarts. 2016

Learning Rate Schedule：学习率调整策略

# Linear Scale

# Warmup

# Decay

# Linear + Warmup + Decay

Linear Scale

Warmup

Decay

Linear + Warmup + Decay