K-Means聚类算法原理及Python实践

鲁老师大约 6 分钟

“聚类”（Clustering）试图将数据集中的样本划分为若干个不相交的子集，每个子集被称为一个“簇”或者“类”，英文名为Cluster。比如鸢尾花数据集（Iris Dataset）中有多个不同的子品种：Setosa、Versicolor、Virginica，不同品种的一些观测数据是具有明显差异的，我们希望根据这些观测数据将其进行聚类。

下图可以看到，不同品种的鸢尾花的花萼（Sepal）和花瓣（Petal）长度和宽度存在明显的差异。花萼长度（Sepal Length）、花萼宽度（Sepal Width）等观测数据可以作为样本的特征，用来进行聚类分析。

不同鸢尾花的花萼长度和宽度不同

形式化地说，一个样本集D包含m个样本，每个样本有n维特征，聚类算法根据n维特征数据中的一些潜在数据分布，将样本集D分为k个不相交的簇。需要注意的是：**聚类过程是机器算法自动确定分类的过程，机器所确定的分类与真实分类之间的语义联系需要使用者把握。**总之，聚类是一种非监督学习（Unsupervised Learning），我们可以不用事先确定一个样本到底分到哪一类，机器会从样本的特征数据中发现一些潜在模式，最终将相似样本归结到一起。

K-Means算法

K均值（K-Means）算法是最常用的聚类算法。

K-Means算法的伪代码来源：周志华《机器学习》

上图为周志华老师《机器学习》一书给出的伪代码，用数学语言表示这个算法，看起来有些缭乱，但其算法思想很简单。假如我们想把数据集D划分为K个簇，大致需要以下几步：

在数据集D中随机选择K个点，这K个点表示K个簇的中心点，即伪代码第1行。
计算数据集D中各个数据应该被分到哪些簇：具体而言，计算样本中所有点距离这K个中心点的距离，将某个样本x划分到距离其最近的中心点对应的簇上，如伪代码的4-8行。
优化当前的聚类结构：对于刚刚生成的分类簇，重新计算簇的中心点，如伪代码的9-16行。
重复前面两步，直到我们得到一个满意的结果。

K-Means算法是一种采用贪心思想的迭代算法。下图展示了从初始状态开始进行的4次迭代，每次迭代，簇的中心点和簇内数据点也在变化。

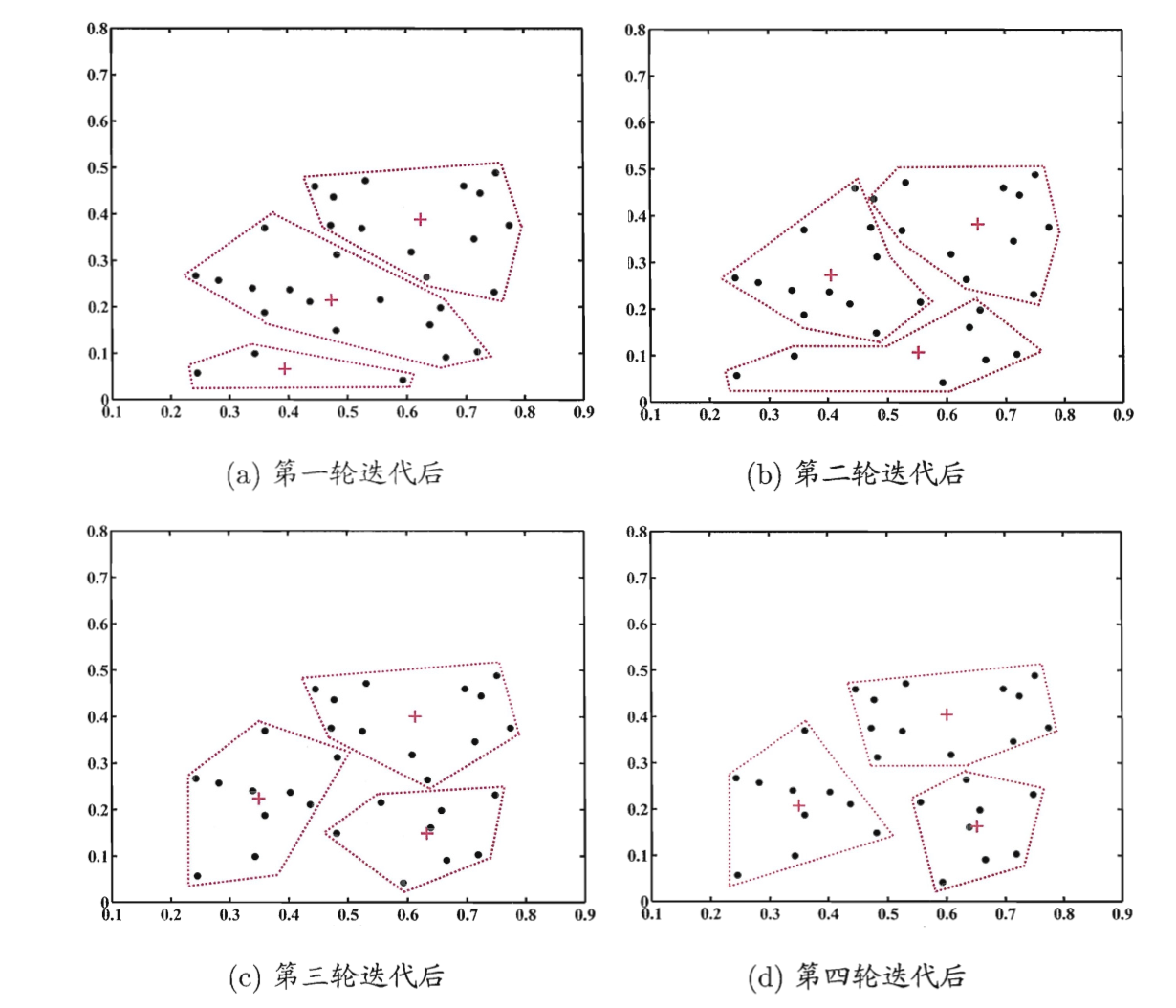
将数据集分为3个簇，四轮迭代的结果，样本点为“·”，簇中心点为“+” 来源：周志华《机器学习》

使用scikit-learn对Iris数据集进行聚类

Iris数据集共有3种类别的鸢尾花，每种50个样本。数据集提供了4个特征：花萼长度（Sepal Length）、花萼宽度（Sepal Width）、花瓣长度（Petal Length）和花瓣宽度（Petal Width）。

数据探索

from sklearn import datasets
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.cluster import KMeans

iris = datasets.load_iris()

### 对数据集进行探索
# 打印数据集特征
print("特征名：" + str(iris.feature_names))

# 探索一个样本数据，每行数据4列，分别表示上述4种特征
print("第一行样本：" + str(iris.data[:1]))

# 第一个样本属于哪个品种，用数字代号表示
print("第一行样本所属品种：" + str(iris.target[:1]))

打印结果为：

特征名：['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
第一行样本：[[5.1 3.5 1.4 0.2]]
第一行样本所属品种：[0]

对花萼长度和宽度这两维数据进行可视化：

# 查看前两列数据，即花萼的长度和宽度
X = iris.data[:, :2]
y = iris.target

# 将数据集中所有数据进行二维可视化展示
plt.scatter(X[:,0], X[:,1], c=y, cmap='gist_rainbow')
plt.xlabel('Spea1 Length', fontsize=12)
plt.ylabel('Sepal Width', fontsize=12)

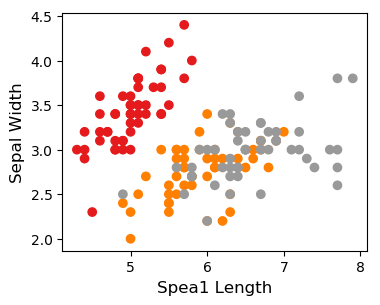
花萼长度和宽度散点图可视化

# 为了更好理解数据集，使用PCA建模，观察3D模式下数据的分布
fig = plt.figure(1, figsize=(8, 6))
ax = Axes3D(fig, elev=-150, azim=110)
X_reduced = PCA(n_components=3).fit_transform(iris.data)
ax.scatter(X_reduced[:, 0], X_reduced[:, 1], X_reduced[:, 2], c=y, 
           cmap=plt.cm.Set1, edgecolor='k', s=40)
ax.set_title("PCA建模")
ax.set_xlabel("1st eigenvector")
ax.w_xaxis.set_ticklabels([])
ax.set_ylabel("2nd eigenvector")
ax.w_yaxis.set_ticklabels([])
ax.set_zlabel("3rd eigenvector")
ax.w_zaxis.set_ticklabels([])

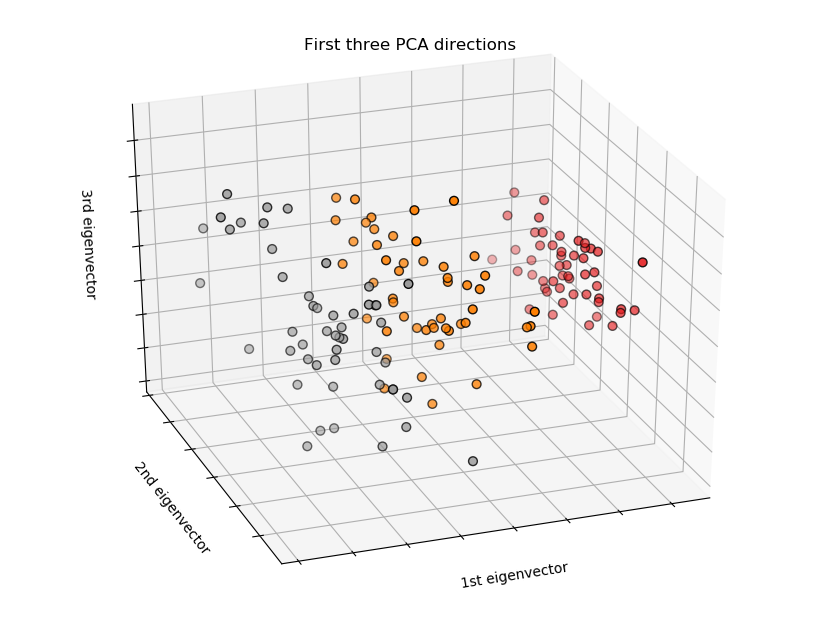
PCA 3D数据分布

通过图表中可以看到：数据集共有三个品种，不同品种的特征分布有一定的模式。

使用K-Means算法进行聚类分析

### 对数据集使用K-Means进行聚类
km = KMeans(n_clusters = 3)
km.fit(X)

# 打印聚类后各个簇的中心点
centers = km.cluster_centers_
print(centers)

数据集被分为3个簇，这三个簇的中心点坐标为：

[[5.006      3.428     ]
 [6.81276596 3.07446809]
 [5.77358491 2.69245283]]

我们可以比较一下K-Means聚类结果和实际样本之间的差别：

# 比较聚类效果与真实品种之间的差异
predicted_labels = km.labels_

fig, axes = plt.subplots(1, 2, figsize=(16,8))
axes[0].scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1, 
                edgecolor='k', s=150)
axes[1].scatter(X[:, 0], X[:, 1], c=predicted_labels, cmap=plt.cm.Set1,
                edgecolor='k', s=150)
axes[0].set_xlabel('Sepal length', fontsize=16)
axes[0].set_ylabel('Sepal width', fontsize=16)
axes[1].set_xlabel('Sepal length', fontsize=16)
axes[1].set_ylabel('Sepal width', fontsize=16)
axes[0].tick_params(direction='in', length=10, width=5, colors='k', labelsize=20)
axes[1].tick_params(direction='in', length=10, width=5, colors='k', labelsize=20)
axes[0].set_title('Actual', fontsize=18)
axes[1].set_title('Predicted', fontsize=18)

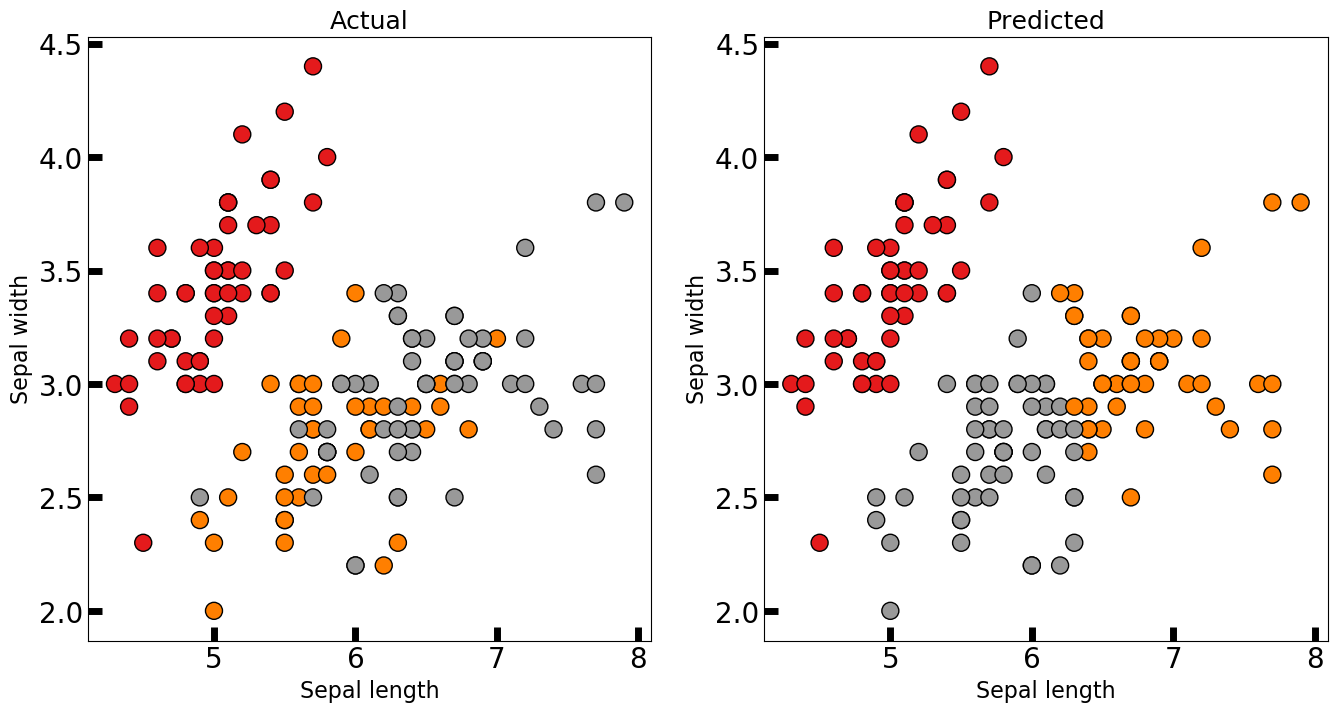
K-Means聚类后，聚类结果和实际样本之间的差别图

左侧是实际情况，右侧是聚类结果，实际结果中橘黄色和灰色类别的两种鸢尾花的数据表现上有一些交叉，聚类算法无法智能到将这些交叉在一起的点区分开来。

K-Means聚类算法原理及Python实践

# K-Means算法

# 使用scikit-learn对Iris数据集进行聚类

# 数据探索

# 使用K-Means算法进行聚类分析

K-Means算法

使用scikit-learn对Iris数据集进行聚类

数据探索

使用K-Means算法进行聚类分析